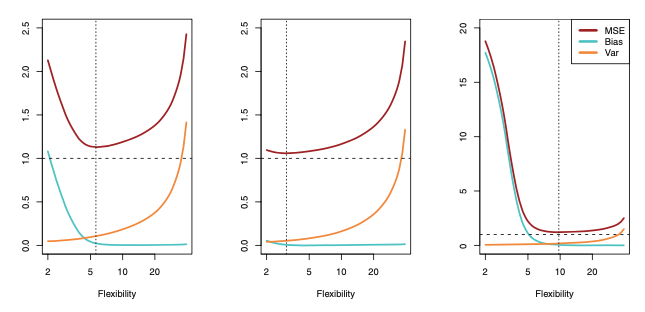
In all three cases, variance increases and bias decreases as the method’s flexibility increases. However, the flexibility level that yields the best test MSE differs among the three data sets. This difference occurs because the squared bias and variance change at different rates in each data set.

In the left-hand panel of the figure, bias decreases rapidly. This causes a sharp drop in the expected test MSE at first.

In the center panel, the true f is close to linear. Here, bias only decreases slightly as flexibility rises. The test MSE declines just a bit before it quickly rises due to increasing variance.

In the right-hand panel, flexibility causes a dramatic drop in bias because the true f is highly non-linear. The variance increases very little as flexibility grows.

As a result, the test MSE falls significantly before a slight increase as model flexibility keeps rising.

The relationship between bias, variance, and test set MSE is called the bias-variance trade-off

Good test set performance requires both low variance and low squared bias. This situation is called a trade-off because it is easy to get a model with extremely low bias but high variance — for example, fitting a curve through every training point. Or, you might get very low variance but high bias — like fitting a horizontal line to all data.

The challenge lies in finding a method where both variance and squared bias remain low.

The post Relationship between bias, variance, and test set MSE appeared first on Alpesh Kumar.